Diese Seite funktioniert nur mit Javascript.
Angebotsfunktion3.5.1 Angebotsfunktion einer UnternehmungKurz- und langfristige Angebotsfunktion
ill man ermitteln, welche Produktionsmenge den Gewinn $G$ der Unternehmung maximiert, muss man betrachten, wie sich Umsatz $U$ und Kosten $C$ mit der Produktion $x$ verändern.
$$ G(x) = U(x) - C(x) \tag{1} $$In den vorigen Abschnitten wurde die Kostenfunktion $C(x)$ hergeleitet und ausführlich diskutiert. Was den Umsatz betrifft, ist eigentlich nicht viel mehr zu sagen, als dass er sich für die Konkurrenzunternehmung angeben lässt als Preis mal Absatzmenge:
$$ U(x) = p_x \cdot x \tag{2} $$Dabei sei an Folgendes erinnert: Erstens, die Preise können durch die Unternehmung nicht beeinflusst werden. Zweitens wird angenommen, dass die Produktion unmittelbar und vollständig abgesetzt werden kann. Damit gilt, dass jede zusätzlich produzierte Einheit eine Umsatzsteigerung in Höhe des Preises auslöst. Hierfür wurde im Zusammenhang mit der direkten Preiselastizität der Nachfrage der Begriff Grenzumsatz eingeführt. Er ist für die Unternehmung bei vollkommener Konkurrenz immer gleich dem Preis. Aus ihrer Perspektive ist der Markt "unendlich" groß und die Nachfrage vollkommen elastisch (vgl. a. Amoroso-Robinson-Relation).
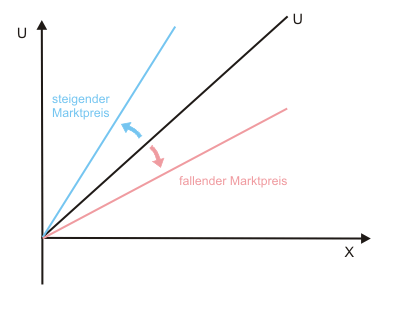
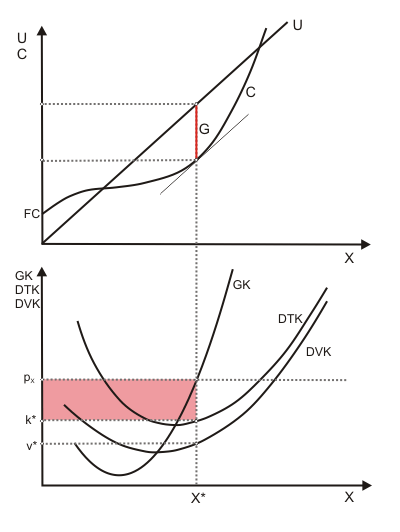
Der Umsatz lässt sich in Abhängigkeit von der Produktionsmenge (= Absatzmenge) als Gerade durch den Ursprung darstellen (Abbildung 1).
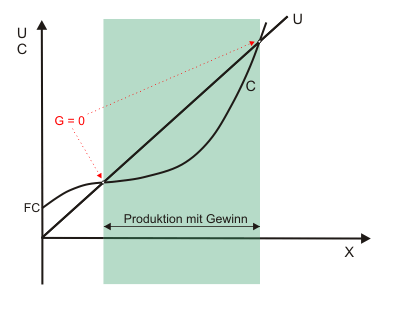
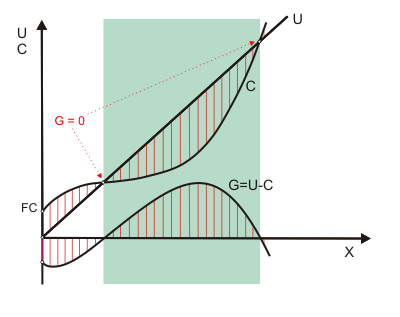
Wird nun die Kostenfunktion der Abbildung hinzugefügt, kann man den Gewinn für alternative Produktionsmengen als senkrechten Abstand zwischen Umsatz- und Kostenfunktion ablesen. Abbildung 2 zeigt für einen klassischen Kostenverlauf mit dem grün hinterlegten Bereich alle Produktionsmengen, die nicht zu einem Verlust führten. Aus der in Abbildung 2 wiedergegebenen Kostenfunktion kann übrigens auf eine kurzfristige Betrachtung geschlossen werden, da fixe Kosten in Höhe FC anfallen.
Um das Gewinnmaximierungsproblem grafisch zu lösen, kann man die senkrechten Abstände zwischen Umsatz- und Kostenfunktion ausmessen und als Gewinnfunktion darstellen (Abbildung 3). Der höchste Gewinn findet sich offenbar dort, wo die Gewinnfunktion eine Steigung von null zeigt. Allerdings ist das, wie man aus Abbildung 3 erkennen kann (dazu Mauszeiger über die Grafik stellen), nur eine notwendige, jedoch keine hinreichende Bedingung für ein Gewinnmaximum. Auch bei einem Verlustmaximum (= Gewinnminimum) ist die Steigung der Gewinnfunktion gleich null. Es ist also zusätzlich zu überprüfen, ob die Steigung der Gewinnfunktion mit steigender Produktion abnimmt. Das ist nur beim Gewinnmaximum der Fall.
Sie versthen nur Bahnhof?
Sie haben die Herleitung dieser wichtigen Regel nicht verstanden? Dann klicken Sie hier für eine Erklärung zum langsamen Mitdenken.
Die grafische Betrachtung liefert die entscheidenden Hinweise für das analytische Vorgehen. Die erste Ableitung der Gewinnfunktion nach der Produktionsmenge muss null, ihre zweite Ableitung negativ sein. Zunächst wird in Gleichung (1) der Umsatz durch den Ausdruck in (2) ersetzt
$$ G(x) = p_xx - C(x) \tag{3} $$und anschließend die erste Ableitung gleich null gesetzt
$$ \cfrac{\text{d}G}{\text{d}x} = p_x - \cfrac{\text{d}C}{\text{d}x} {\overset{!}{=}} 0 \tag{4} $$ $$ p_x = \cfrac{\text{d}C}{\text{d}x} \tag{5} $$Damit kann als notwendige Bedingung für ein Gewinnmaximum festgehalten werden:
Um sicher zu gehen, dass die notwendige Bedingung kein Gewinnminimum beschreibt, wird die zweite Ableitung berechnet:
$$ \cfrac{\text{d}^2G}{\text{d}x^2} = -\cfrac{\text{d}^2C}{\text{d}x^2} {\overset{!}{<}} 0 \space\space\space\space \Rightarrow \space\space \cfrac{\text{d}^2C}{\text{d}x^2} {\overset{!}{>}} 0 \tag{6} $$Die Grenzkosten müssen also steigen.
Wie kann man die Regeln inhaltlich interpretieren? Wenn das Unternehmen die Produktion um eine Einheit ausdehnt, steigt der Umsatz um den Produktpreis. Die Kosten steigen um die Grenzkosten. Liegen die Grenzkosten unter dem Preis, so steigt der Gewinn durch die weitere produzierte Einheit. Wenn die Grenzkosten - wie die hinreichende Bedingung fordert - steigen, wird die nächste Produkteinheit den Umsatz zwar wieder um den Preis steigen lassen, aber zu einem stärkeren Anstieg der Kosten führen. Erst wenn die Kosten durch die letzte produzierte Einheit um den Betrag des Preises steigen, lohnt sich eine weitere Ausdehnung der Produktion nicht mehr. Umgekehrt, wenn der Preis unter den Grenzkosten läge, würde sich natürlich eine Verminderung der Produktion positiv auf den Gewinn auswirken. In einfacher Sprache:
So einfach ist das! Ökonomen drücken es halt nur etwas komplizierter aus.
Da spielt es keine Rolle, ob der Unternehmer die Preis-Grenzkosten-Regel kennt. Wenn er Produkte genau dann herstellt, wenn es sich für ihn lohnt, dann hält er sich an diese Regel - ob er ihr bewusst folgt oder auch nicht.
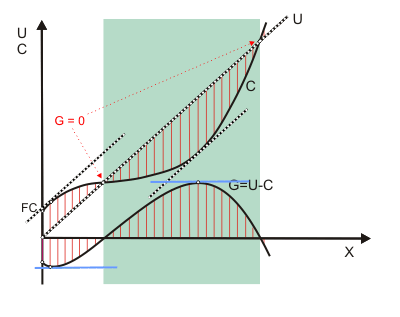
Die "Preis-Grenzkosten-Regel" kann man in Abbildung 4 im oberen Diagramm als Übereinstimmung der Steigungen von Kostenfunktion (= Grenzkosten) und Umsatzfunktion (= Preis) erkennen.
Im unteren Diagramm kann man in einer maßstabsgetreuen Grafik eine Parallele zur Abszisse in Höhe des Produktpreises einzeichnen. Ihr Schnittpunkt mit der Grenzkostenkurve zeigt die gewinnmaximierende Produktionsmenge. Da die Konstruktion eines solchen Doppeldiagramms, in dem dann "tatsächlich alles zueinander passt", recht aufwendig ist, skizziert man die Diagramme meistens einzeln.
Wird die Grenzkostenfunktion von der Preisgeraden im fallenden Bereich geschnitten, ist die hinreichende Bedingung für ein Gewinnmaximum nicht erfüllt, denn die Grenzkosten sinken mit zunehmender Produktion. Natürlich kann es auch vorkommen, dass gar kein (inneres) Gewinnmaximum existiert. Das ist z.B. dann der Fall, wenn die Grenzkosten immer fallen. Aus den Überlegungen zum Zusammenhang von Grenz- und Durchschnittskosten ist bekannt, dass fallende Grenzkosten sinkende Durchschnittskosten bedeuten. Das Produkt kann daher um so kostengünstiger angeboten werden, je mehr hergestellt wird (Gesetz der Massenproduktion). Die Produktion wird kurzfristig an der Kapazitätsgrenze erfolgen, vorausgesetzt der Preis deckt die variablen Kosten.
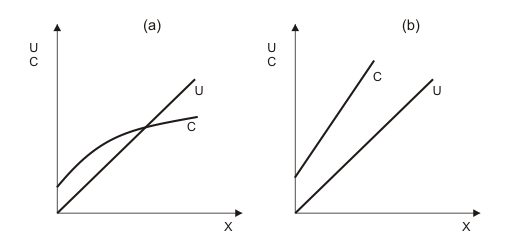
Der Fall sinkender Grenzkosten ist in Abbildung 5a skizziert. Abbildung 5b zeigt konstante Grenzkosten. Stimmen Sie mit dem Preis überein, dann ist die optimale Produktionsmenge unbestimmt. Liegen sie unter dem Preis, wird an der Kapazitätsgrenze produziert. Wenn sie den Preis übersteigen (die dargestellte Situation), lohnt sich die Produktion nicht.
Ein Gewinnmaximum kann also nur für den Fall steigender Grenzkosten berechnet werden. Ansonsten ist die hinreichende Bedingung für ein Gewinnmaximum nicht erfüllt und es kommt zu einer Randlösung, so dass entweder gar nicht oder an der Kapazitätsgrenze produziert wird. Steigende Grenzkosten liegen dann vor, wenn die Skalenelastizität der Produktionsfunktion unter 1 liegt, m.a.W. bei abnehmenden Skalenerträgen (vgl. die Ausführungen zum Zusammenhang zwischen Kosten- und Niveauproduktionsfunktion). Beim klassischen Ertragsgesetz ist dies nur im III. Bereich gegeben. Bei neoklassischen Produktionsfunktionen, wie z.B. der Cobb-Douglas-Funktion $x = K^{0,3}L^{0,6}$, trifft dies durchgängig zu.
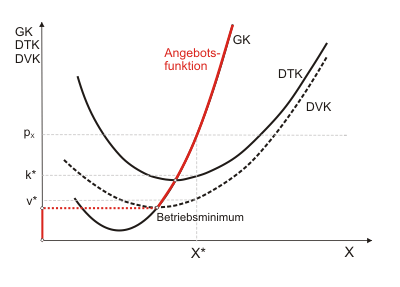
Die eigentliche Angebotsfunktion kann man nun im unteren Diagramm von Abbildung 4 erkennen. Da sich der gewinnmaximierende Unternehmer nach der Preis-Grenzkosten-Regel richtet, kann man für jeden ihm vom Markt vorgegebenen Preis über die Grenzkostenfunktion die optimale Produktionsmenge ablesen.
Dieser Bereich ist in Abbildung 6 rot hervorgehoben.
Die Beschränkung auf den aufsteigenden Ast muss wegen der hinreichenden Bedingung für ein Gewinnmaximum erfolgen. Im fallenden Bereich können nur Gewinnminima auftreten. Unterhalb des Betriebsminimums wird die Unternehmung auch kurzfristig die Produktion einstellen, so dass die optimale Angebotsmenge auf null springt (das ist hier eingezeichnet, unterbleibt aber oft).
Die Tatsache, dass nur der aufsteigende Ast der Grenzkostenfunktion als Angebotsfunktion in Frage kommt, bedingt, dass das geplante Angebot der einzelnen Unternehmung mit steigendem Preis zunimmt. Das wird analog zum Gesetz der Nachfrage als Gesetz des Angebots bezeichnet. Daneben findet sich noch ein weiterer Grund für ein mit dem Preis wachsendes Angebot: Selbst wenn infolge technischer Besonderheiten die einzelnen Unternehmen bei steigenden Preisen die Produktion nicht ausdehnen könnten, würde das Marktangebot wahrscheinlich zunehmen, da die durch die höheren Preise steigenden Gewinne Wettbewerber in den Markt locken würden.
Da die Angebotsfunktion der Grenzkostenfunktion entspricht, lässt sich eine oben abgeleitete Eigenschaft der Grenzkostenfunktion unmittelbar auf die Angebotsfunktion übertragen: Die Fläche unter der Angebotsfunktion zeigt die variablen Kosten der Unternehmung. Das konnte auch schon im einführenden Zahlenbeispiel zum Dingermarkt beobachtet werden.
Nach ähnlichen Seiten im WWW suchen